作为大多数的普通人如何成为千万富翁

前言

此文我只讲底层逻辑，这个底层逻辑还是我个人认为的底层逻辑，所以所有观点都为个人观点和思想出发。这篇文章针对一些迷茫中的职场人士和一些刚进入大学里的大学生们或刚毕业的且刚步入社会的青年小伙伴，还有一些为孩子所操劳的父母们。

阅读此文请拥有此共识：财富一定会流向创造财富的地方去，文明也一定会汇集在高度文明发达之地。

本文定义的普通人（月入<1万）

财富

简单来说就两个地方：掠夺和创造

创造财富简单来说也是两个地方：生成资料和生产力

这里扪心自问一下，你有什么生产力和生产资料。那么既然作为普通人生产力和生产资料没多大差异性，基本上大同小异。如果你有一些差异性那么你就会在普通人中脱颖而出。这个差异性我相信有些人是有的，可能自己没有发觉，有些发觉了但是没有突出这个差异性给自己带来利益。

例如： 有一部分人打游戏很厉害，这一部分人属于少数，那么这一部分少数人中又有一些人因为乱七八糟的事情或着各种各样的条件限制导致自己无法专心走这一条路。但是却也有少比例的人走上了职业、代练、技术主播的路线。为什么我要说技术主播呢，因为直播不只有技术主播这一条路，直播是一个娱乐为主导内容的行业，那么能给观看直播的观众带来节目效果的直播内容也能在直播这条路脱颖而出。所以找寻自己在大多数人中突出的点，然后增长长板，让优势更加巨大，在大多数人中脱颖而出。

少数就是少数，我不认为我属于少数，我也不认为我就特别，所以我就聊聊如何通过普通人达到资产千万

那么除掉差异性之外，对所有人都公平的是什么？

时间：每天就24小时，每小时就60分钟，每分钟就60秒，绝对公平
公理和公式：所有的数学、物理、化学等理工科定理机会对所有人都是公平的
股指基金：它涨 1% 那么它对所有人涨 1%，跌1% 同样所有人都跌 1%

那么股指基金我个人认为最好的是哪些？

标准普尔500

道琼斯

纳斯达克

为什么选股指

那么就有小伙伴要问了，为什么选它？为什么不选股票？

这个问题其实蛮简单的，当你选了一支股票，这支股票涨 8% 那么你就收获 8% ，如果股票跌了 8% ，那么你就亏损了 8%。所以个别股票对所有人而言不是绝对公平的。

比如说，它对它的股东和它对你而言、它对它公司的高管和它对你而言。你觉得作为普通人的你，信息源有他清楚吗？你觉得你做出决策的时间能比他及时吗，你觉得他的涨幅对你和对他也是公平的吗？

那么在此我提出一个赌场问题给你思考一下。

A有100万筹码，你有1万筹码。
每轮游戏时，两人各自抽一张牌，抽到“大”一方可以赢得对方筹码的一半，抽到“小”则无变化。
游戏继续进行，直到某一方破产

结论其实也很显而易见，A基本稳赢，这就是一个简单的概率问题。所以你对于某些股票而言，最后获取利润的概率最大的人就是你们嘴中说到的庄家的那帮人。但是三大指数没有人可以操作得动，甚至以现在的各种庄家的体量而言，市值3000亿美金以上的股票也几乎没有任何一家机构可以操作得动，所以建议要么买股指基金要么买巨头(苹果、英伟达、meta)。

根据我们本文的共识，理论上在一个正常的股市是聚集不断创造新财富公司的地方，那么这个地方一定是上涨的。那么事实上近30年：

标普500（近30年）：年化 12.2% （ps：近10年 4倍多）

道琼斯（近30年）：年化9.2% （ps：近10年 3倍多）

纳斯达克（近30年）：年化13.5% （ps：近10年 6倍多）

既然年化这么好为什么还是有人不买呢，还是人性，贪嗔痴。想要更多。赌徒心理，成为韭菜

快则慢，慢则快

只需要等待，等花开

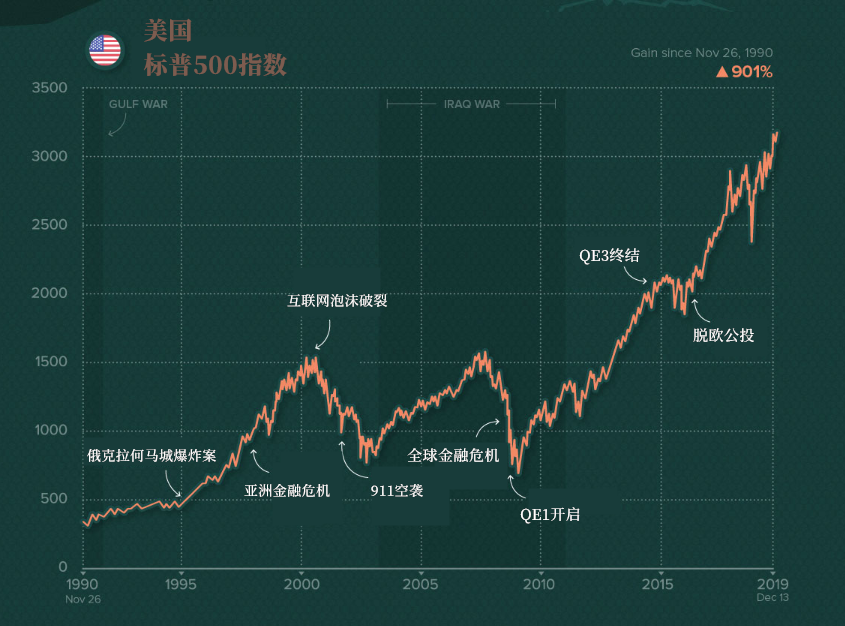
过去30年全球七大股市的成绩单-市场参考-金十数据

从长期来看持有正规股市股票的伙伴们你们一定会收到上涨的财富。

回归主题，现在我们有对所有人都公平的时间，它是我们生产资料之一。第二、投资股指基金的机会，它也是我们的生产资料之一。第三、一些数学公理等

成为千万富翁

你是愿意背30年房贷还是愿意忍受30年成为千万富翁（详细见后面数学公式）

30年后都五六十了，有这些钱有什么用？

可是有多少人到五六十了连100万都没有，但是你拿的是1000万能很快到手到现钱

存不下来钱怎么办？

推荐一本书：《邻居的百万富翁》

给我激励存钱的一段话如下图

大致翻译如下：

1
2
3
4
5
6
7


赚到第一笔10万美元跟个婊子一样难受，但你必须做到。
我不管你得付出什么——如果需要，步行出门，
吃的东西也只能是靠优惠券买的，
总之，想办法搞到那10万美元。
等你有了第一桶金，接下来就可以稍微放松一点了。

查理·芒格

The Forex Complex on X: “Charlie Munger once said: “The first $100,000 is a bitch, but you gotta do it.” Here are his 5 money rules to make your first $100k (without

我想，作为理性且聪明的你已经有答案。

根据以上的内容我们拥有了时间、投资股指基金的机会、数学公理，那么现在我们去实现它，让一个普通人30年成为千万富翁

公式解释：

复利公式用于计算定期存入一定金额（例如每月、每年）的投资或储蓄在未来的总金额。这个公式考虑了定期存入本金和利息不断复利积累的情况。

公式：

$$ FV = P \times \left(1 + \frac{r}{n}\right)^{nt} \times \frac{\left(1 + \frac{r}{n}\right)^{nt} - 1}{\frac{r}{n}} $$

其中：

$FV$：未来价值（最终金额）
$P$：每期存入的金额（例如每月存入的金额）
$r$：年利率（以小数表示，如 5% 就是 0.05）
$n$：每年复利的次数（例如每月复利时，$n = 12$）
$t$：投资的总时间（单位：年）

例子：每月存入 3000 元，月复利，30 年

假设：

每月存入金额 $P = 3000$ 元
年利率 $r = 0.05$（5%）
每年复利次数 $n = 12$（每月复利）
投资年数 $t = 30$ 年

步骤 1：计算

$$ \left(1 + \frac{r}{n}\right)^{nt} $$

首先，计算每月的利率：

$$ \frac{r}{n} = \frac{0.05}{12} = 0.004167 $$

然后，计算复利项：

$$ \left(1 + \frac{r}{n}\right) = 1 + 0.004167 = 1.004167 $$

接着，计算复利的次数 $nt$：

$$ nt = 12 \times 30 = 360 \text{（即 30 年，共 360 个月）} $$

计算复利项的指数：

$$ 1.004167^{360} \approx 4.4677 $$

步骤 2：计算

$$ (\frac{\left(1 + \frac{r}{n}\right)^{nt} - 1}{\frac{r}{n}}) $$

计算差值部分：

$$ \left(1.004167^{360} - 1\right) = 4.4677 - 1 = 3.4677 $$

然后，计算：

$$ \frac{3.4677}{0.004167} \approx 831.141 $$

步骤 3：计算未来价值 $FV$

现在，可以代入所有值来计算未来价值：

$$ FV = 3000 \times 4.4677 \times 831.141 \approx 3000 \times 3720.146 = 11,160,438 $$

未来价值（$FV$）约为 11,160,438 元。

复利的威力：

从上面的例子可以看到，尽管你每月只存入 3000 元，但由于复利的效应，在 30 年后，投资额的增长非常显著。这是因为每个月的利息不仅会让本金增值，还会让之前产生的利息继续产生利息，形成正向循环。

复利的威力体现：

时间的作用：复利的威力在于时间的积累，随着投资时间的增长，复利的效应会越来越强。短期内，你可能看不出明显效果，但长期复利会显著增加最终的总金额。
利率的影响：即使是较低的年利率（如 5%），长期复利的效应仍然能让金额快速增长。
定期存入的累积效应：即使每个月存入相对较少的金额，经过 30 年的复利积累，最终的总金额仍然非常可观。

总结：

通过每月定期存入 3000 元，经过 30 年的月复利，最终的金额将达到约 11,160,438 元。复利的关键在于时间和利息的持续积累，这也就是复利被称为“世界第八大奇迹”的原因。

前言

财富